Given the equation
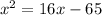
To find a and b, you have to find the roots, following the steps below.
Step 01: Write the equation in the general quadratic form.
The general quadratic form is ax²+bx+c=0.
Then, add -16x + 65 to both sides of the equation.
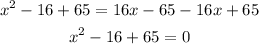
Step 2: Use the Bhaskara formula to find the roots.
The Bhaskara formula for a general equation is:
![x=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2\cdot a}](https://img.qammunity.org/2023/formulas/mathematics/college/uqsn52onz34wdlqp5q7o3d75junrk7u3bj.png)
In this exercise,
a = 1
b = -16
c = 65
Then,
![\begin{gathered} x=\frac{-(-16)\pm\sqrt[]{(-16)^2-4\cdot1\cdot65}}{2\cdot1} \\ x=\frac{+16\pm\sqrt[]{256-260}}{2} \\ x=\frac{+16\pm\sqrt[]{-4}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9tpruluy4dil1gul7p8u22c2uliy3yhn90.png)
√-4 can also be written as:
![\sqrt[]{-4}=\sqrt[]{(4)\cdot(-1)}=\sqrt[]{4}\cdot\sqrt[]{-1}](https://img.qammunity.org/2023/formulas/mathematics/college/px7nxa7m85u20dfdsmvse02esch2d0d14d.png)
Knowing that i = √-1:
![\sqrt[]{-4}=\sqrt[]{4}\cdot i](https://img.qammunity.org/2023/formulas/mathematics/college/uwf62dxbsbhhi29tzkx3pffsablg9c9alb.png)
Then:
![\begin{gathered} x=\frac{+16\pm\sqrt[]{-4}}{2}=\frac{+16\pm\sqrt[]{4}\cdot i}{2} \\ x=(16\pm2\cdot i)/(2) \\ x=(16)/(2)\pm(2)/(2)\cdot i \\ x=8\pm i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2kms2tmgi96jf0kpm2n14ch5sx542pk5w7.png)
The roots are:
8 + 1i
8 - 1i
So, the Answer is:
a = 8
b = 1