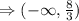Question

B. -3/4x-4=-6C. Is 0 solution to -3/4x-4>-6Select answerYes. No.D. Using interval Notation, solve: -3/4x-4>-6

Answer 1

Step-by-step explanation:

Part A:

The question is given below as

`\begin{gathered} whenx=0,evaluate \\ -(3)/(4)x-4= \end{gathered}`

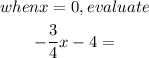
By putting x=0, we will have that

`\begin{gathered} \begin{equation*} -(3)/(4)x-4 \end{equation*} \\ -(3)/(4)(0)-4 \\ =-4 \end{gathered}`

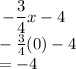
Hence,

The final answer for part A is

`\Rightarrow-4`

Part B:

`\begin{gathered} solve, \\ -(3)/(4)x-4=-6 \end{gathered}`

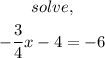
add 4 to both sides

`\begin{gathered} -(3)/(4)x-4=-6 \\ -(3)/(4)x-4+4=-6+4 \\ -(3)/(4)x=-2 \\ coess\text{ multiply, we will have} \\ -3x=-2*4 \\ -3x=-8 \\ divide\text{ both sides by -3} \\ (-3x)/(-3)=-(8)/(-3) \\ x=(8)/(3) \end{gathered}`

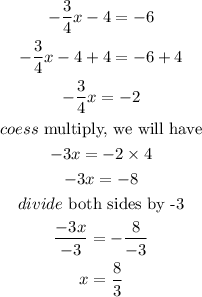
Hence,

The final answer for part B is

`\Rightarrow x=(8)/(3)`

Part C:

`-(3)/(4)x-4>-6`

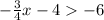
Add 4 to both sides, we will have

`\begin{gathered} -(3)/(4)x-4\gt-6 \\ -(3)/(4)x-4+4\gt-6+4 \\ -(3)/(4)x>-2 \\ cross\text{ multiply} \\ -3x>-2*4 \\ -3x>-8 \\ divide\text{ bth sides by -3} \\ (-3x)/(-3)>-(8)/(-3)(the\text{ sighn will be reversed\rparen} \\ x<(8)/(3)(0\text{ is a solution\rparen} \end{gathered}`

Hence,

The final answer for part C is YES

Part D:

`\begin{gathered} -(3)/(4)x-4\gt-6 \\ -(3)/(4)x-4+4\gt-6+4 \\ -(3)/(4)x>-2 \\ cross\text{ multiply} \\ -3x>-2*4 \\ -3x>-8 \\ divide\text{ bth sides by -3} \\ (-3x)/(-3)>-(8)/(-3)(the\text{ sighn will be reversed\rparen} \\ x<(8)/(3) \\ hence,in\text{ interval notation we will have the final answer be} \\ (-\infty,(8)/(3)) \end{gathered}`

Hence,

The final answer for part D is given below as

`\Rightarrow(-\infty,(8)/(3))`