Question

Notebook paper is approximately 0.004 in. thick. Using the formula for the width W, determine how wide a square piece of notebook paper would need to be successfully fold it in half 13 times , alternating horizontal and vertical folds.

Answer 1

The question has already provided a formula to determine the width (W). The question also provides the thickness as well as the number of times (n) the paper would be folded. Hence, we have;

`\begin{gathered} W=\pi* T*2(3(n-1))/(2) \\ W=3.14*0.004*2*(3(13-1))/(2) \\ W=0.02512*(3(12))/(2) \\ W=0.02512*18 \\ W=0.45216\text{ inches} \end{gathered}`

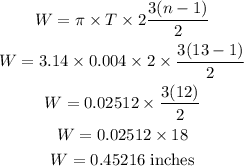
The notebook paper would have to be 0.45216 inches wide

The formula has also been provided that would help in calculating the length of a long rectangular piece of paper. We've been given the thickness of the paper and the number of times it (n) it would be folded. Therefore, we now have;

`\begin{gathered} L=(\pi T)/(6)(2^n+4)(2^n-1) \\ L=(3.14*0.002)/(6)(2^(12)+4)(2^(12)-1) \\ L=0.00104667(4096+4)(4096-1) \\ L=0.00104667(4100)(4095) \\ L=17573.066\text{ inches} \end{gathered}`