Question

A ball is thrown from a height of 70 meters with an initial downward velocity of 10 m/s. The bal's height h (In meters) after t seconds is given by the following.h = 70 - 10-512How long after the ball is thrown does it hit the ground?Round your answer(s) to the nearest hundredth.(If there is more than one answer, use the "or" button.)

Answer 1

2.87secs

Step-by-step explanation:

Given the expression for calculating the height reached by the ball expressed as;

`h(t)=70-10t-5t^2`

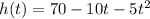
The ball will hit the ground when h(t) = 0.

Substituting into the expression given;

`\begin{gathered} 0=70-10t-5t^2 \\ \text{Rearrange;} \\ 5t^2+10t-70=0 \\ \end{gathered}`

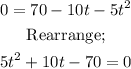
Factorize the resulting equation and find the value of t

`\begin{gathered} t\text{ = }\frac{-10\pm\sqrt[]{10^2-4(5)(-70)}}{2(5)} \\ t=\frac{-10\pm\sqrt[]{100+1400}}{10} \\ t=\frac{-10\pm\sqrt[]{1500}}{10} \\ t=(-10\pm38.73)/(10) \\ t=(-10+38.73)/(10) \\ t=(28.73)/(10) \\ t=2.87\sec s \end{gathered}`

This means that it will take 2.87secs for the ball to hit the ground