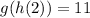Question

Please help me i gotta finish this or else I fail

Answer 1

Question 1

----------------------------------------------------------------------------------------------------------------

(a)(i)

To evaluate f(4), we take the functional value at x = 4.

Looking at the graph, it is:

At x = 4, y = 2 [counting units]

Thus,

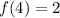`f(4)=2`(a)(ii)

To evaluate f(-3), we take the functional value at x = -3.

Looking at the graph, it is:

At x = -3, y = -5 [counting units]

Thus,

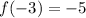
`f(-3)=-5`(b)

The zeros are the x-intercepts of a graph. Looking at the graph, the x-axis cutting points are:

Zeros

`x=2,x=-5`(c)

The function f(x) is increasing where the slope of the graph is positive.

Looking at the graph, the increasing part is from x = -3 to x = 5.

That is

- 3 < x < 5

The correct choice is (2).

(d)

The relative minimum is the lowest point of the graph shown and the relative maximum is the highest point of the graph.

Looking at the graph,

The lowest point occurs at --- (-3, -5)

The highest point occurs at --- (-7, 5)

So,

Relative Maximum: (-7, 5)

Relative Minimum: (-3, -5)

(e)

We want the interval in which f(x) < 0.

This means where the function is less than zero, or below the x-axis.

Looking at the graph,

from x = -5 to x = 2, the graph of f(x) is below the x-axis.

That is -5 < x < 2.

The correct choice is (3).

(f)

A new function --

`g(x)=2f(x)+5`

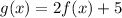
Let's evaluate g(0) by using the formula:

`g(0)=2f(0)+5`

From the graph, f(0) = -2, thus,

g(0) = 2(-2) + 5

g(0) = -4 + 5

g(0) = 1

This means that the functional value of 'g' is 1 at x = 0.

(g)

A new function --

`h(x)=x^3-3`

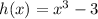
We need to find g(h(2)). Let's boil it down to the function f(x).

`\begin{gathered} h(x)=x^3-3 \\ h(2)=2^3-3 \\ \therefore h(2)=5 \\ \text{Now, we need g(5).} \\ g(x)=2f(x)+5 \\ g(5)=2f(5)+5 \\ g(5)=2(3)+5 \\ g(5)=6+5 \\ g(5)=11 \\ \text{ Final answer:} \\ g(h(2))=11 \end{gathered}`

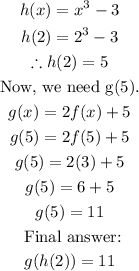
Thus, the answer is:

`g(h(2))=11`