Question

Determine the distance between the two points (-1,-9) and (4,-7)What is the midpoint of the line segment joining the pairs of Points.

Answer 1

Step-by-step explanation

Finding the distance between the points

The distance between two points (x₁,y₁) and (x₂,y₂) is given by the following formula.

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

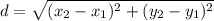
Then, we have:

`\begin{gathered} (x_1,y_1)=(-1,-9) \\ (x_2,y_2)=(4,-7) \end{gathered}`
`\begin{gathered} d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ d=(4-(-1))^2+(-7-(-9))^2 \\ d=(4+1)^2+(-7+9)^2 \\ d=√(5^2+2^2) \\ d=√(25+4) \\ d=√(29) \\ d\approx5.4 \\ \text{ The symbol }\approx\text{ is read 'approximately'.} \end{gathered}`

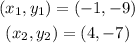
Finding the midpoint of the line segment joining the points

The midpoint of the line segment P(x₁,y₁) to Q(x₂,y₂) is:

`\text{ Midpoint }=((x_1+x_2)/(2),(y_1+y_2)/(2))`

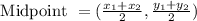
Then, we have:

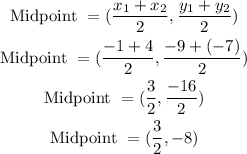
`\begin{gathered} \text{ Midpoint }=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ \text{ Midpoint }=((-1+4)/(2),(-9+(-7))/(2)) \\ \text{ Midpoint }=((3)/(2),(-16)/(2)) \\ \text{ Midpoint }=((3)/(2),-8) \end{gathered}`Answer

The distance between the given points is √29 units or 5.4 units rounded to the nearest tenth.

The midpoint of the line segment that joins the pairs of points is (3/2,-8).