Given in the question:
a.) A washer and a dryer cost $649 combined.
b.) The washer costs $51 less than the dryer.
From the given description, let's transform them into an equation.
Let,
x = Cost of washer
y = Cost of dryer
a.) A washer and a dryer cost $649 combined.
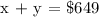
b.) The washer costs $51 less than the dryer.
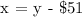
From the generated equation, substitute x = y - $51 to x + y = $649.
We get,
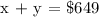
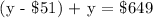
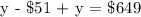
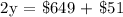
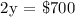
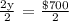
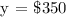
Therefore, the cost of the dryer is $350.
Let's find the cost of the washer.
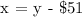
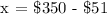
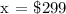
Therefore, the cost of the washer is $299.