The slope of a line
Given two points through which a line passes A(x1,y1), B(x2,y2), the slope of the line can be calculated with the formula:

We are given the point A(-4,-8) and the (incomplete) point B(?,1). Knowing the slope is m=2, we can calculate the missing value at point B. Let's call it x: B(x,1).
Substituting all the values in the formula of the slope, we get:

Operating:
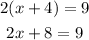
Solving for x:
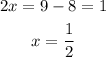
The missing value is 1/2, thus point B is B( 1/2 , 1 )