Question

Find the average rate of change for the function : g(x) = 3x^2 over the interval (2,4)

Answer 1

Given the function below;

`g(x)=3x^2`

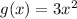
To calculate the average rate of change for the given function over a given interval, we shall apply the following formula;

`(\Delta f)/(\Delta x)=(f(x_2)-f(x_1))/(x_2-x_1)`

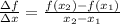
Where the variables are as follows;

`\begin{gathered} x_1=2 \\ x_2=4 \end{gathered}`

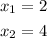
Let us now evaluate the function at each input value;

`\begin{gathered} g(x_1)=g(2)=3(2)^2 \\ g(x_1)=g(2)=3*4 \\ g(x_1)=g(2)=12 \end{gathered}`

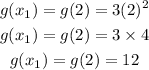
Also, for the second input value;

`\begin{gathered} g(x_2)=g(4)=3(4)^2 \\ g(x_2)=g(4)=3*16 \\ g(x_2)=g(4)=48 \end{gathered}`

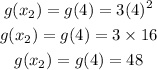
We can now substitute the values into the formula above, and we'll have;

`\begin{gathered} (\Delta g)/(\Delta x)=(g(x_2)-g(x_1))/(x_2-x_1) \\ =(48-12)/(4-2) \\ =(36)/(2) \\ =18 \end{gathered}`

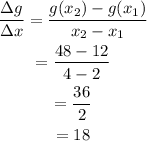
Therefore the average rate of change of the function;

`g(x)=3x^2`

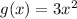
Over the interval,

`(2,4)`

ANSWER:

18