Given:
• Cyclist A:
Starting position = 10 m
Gets to 60 m in 10 seconds
• Cyclist B:
Starting position = 60 m at 0 seconds
Gets to starting position in 10 seconds
Let's estimate the time at which the two cyclists pass each other.
Let's find the velocity of each cyclist:
Velocity of cyclist A:

Velocity of cyclist B:
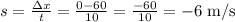
Now, let's write the motion of each cyclist as an equation:
Cyclist A: y = 5x + 10
Cyclist B: y = -6x + 60
Where x represents the time and y is the position.
Now, let's solve both equations simultaneously:
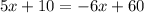
Now, let's solve for x.
Move all terms with the variable x to the left
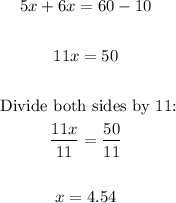
Therefore, the time at which the two cyclists will pass each other is 4.54 seconds
• ANSWER:
4.54 seconds