Answer:
x = 1
y = 2
z = -1
Step-by-step explanation:
We have the system:
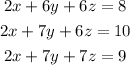
We can use the Elimination Method. We'll try to eliminate variables from any of the equations by adding or resting the other equations.
First, if we subtract the 3º equation to the 1º one:
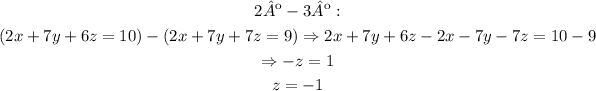
Now we know the value of z.
Next, we can subtract the 1º equation to the 2º:
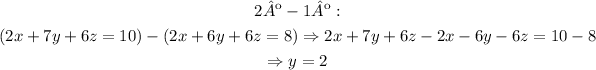
The value of y = 2
Now, we can use the values of z and y, to find the value of x. Let's use the 1º equation:
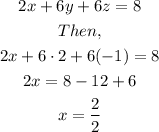
x = 1
We have found the solution of the equation system:
x = 1
y = 2
z = -1