Question

Perform the indicated operation. 6/x+7 + 3/x-4

Answer 1

The question asks us to perform the following operation:

`(6)/(x+7)+(3)/(x-4)`

This just requires us finding the LCM of both fractions and multiplying top and bottom of both fractions by the LCM.

The LCM of both fractions is the multiplication of their denominators. i.e.

`\text{LCM}=(x+7)(x-4)`

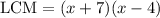
Hence, we can continue with the solution:

`\begin{gathered} (6)/(x+7)+(3)/(x-4) \\ \text{ multiply top and bottom by the LCM} \\ \mleft((6)/(x+7)+(3)/(x-4)\mright)*((x+7)(x-4))/((x+7)(x-4)) \\ \\ (6)/(x+7)*((x+7)(x-4))/((x+7)(x-4))+(3)/(x-4)*((x+7)(x-4))/((x+7)(x-4)) \\ \\ (6(x-4))/((x+7)(x-4))+(3(x+7))/((x+7)(x-4)) \end{gathered}`

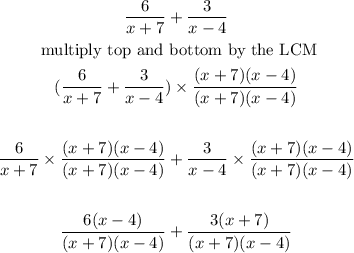
At this time, both denominators are equal, hence we can add the numerators of both fractions under their common denominator

Continuing with the solution:

`\begin{gathered} (6(x-4)+3(x+7))/((x+7)(x-4)) \\ \text{Expand the numerator brackets} \\ (6x-24+3x+21)/((x+7)(x-4)) \\ (6x+3x-24+21)/((x+7)(x-4)) \\ \\ (9x-3)/((x+7)(x-4)) \\ Expand\text{ the denominator brackets} \\ \\ \frac{9x-3}{x(x)-4(x)+7(x)+7(-4)^{}} \\ (9x-3)/(x^2-4x+7x-28) \\ \\ \therefore(9x-3)/(x^2+3x-28)\text{ (Option 2 IS THE FINAL ANSWER)} \end{gathered}`