Question

What is the surface area of the triangular prism (Look at image)

Answer 1

`\Large \boxed{\sf 384 \ m^2}`

Explanation:

Surface area ⇒ area of 2 triangles + area of 3 rectangles

`(8 * 3 * 0.5 * 2)+(20 * 5 * 2+20 * 8)=384`

Answer 2

Geometric Solids: Prism

For a prism we take into account the following:

• 
  `\boxed{\bold{Lateral\ area = (Perimeter \ of \ the \ base) (height)}}`

• 
  `\boxed{\bold{Total\ area = Lateral\ area + 2 (base\ area)}}`

Taking into account the above, we first find the lateral area:

In the triangular base, the height divided into 2 small right triangles of Hypotenuse = 5 and Height = 3. By Pythagoras we have this:

3² + base² = 5²

9 + base² = 25

base² = 25 - 9

base² = 16

base = 4

From this we obtain that the bases of the small right triangles measure 4 therefore the triangular base is isosceles where we have:

• Equal sides = 5

• Uneven side = 8

The perimeter of the triangular base will be the sum of the sides, that is:

Perimeter = 5 + 5 + 8

⇒ Perimeter = 18

Since the perimeter of the base of the prism is 18 and the height is 20, we replace in the equation for the lateral area:

Side area = (18) (20)

⇒ Lateral Area = 360 m²

Now we find the area of ​​the triangular base with base = 8 and height = 3:

`\bold{Area=((base) (height))/(2) }\\\\\\Area=((8)(3))/(2) \\\\\\Area=(24)/(2)\\\\\\\boxed{\bold{Area=12}}`

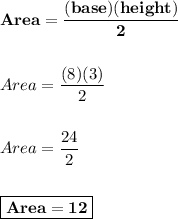
Since we have that the lateral area is 360m² and the area of ​​the triangular base is 12m², we replace in the equation of the total area:

Total area = 360 + 2 (12)

Total area = 360 + 24

Total area = 384 m²

The total area of ​​the prism will measure 384m²

I hope I have helped you, greetings from Venezuela!