The interest formula is :
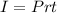
where I = interest
P = Principal amount
r = interest rate
t = time in years
From the problem, Susan invested twice the amount at 6% as she does at 5%.
If she invested P to 5%, the amount she invested to 6% will be 2P
Using the formula to calculate the two interests.
For 5% :
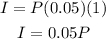
For 6% :

The sum of the interests is $510
This will be :

She invested $3000 for 5% and $6000 for 6%
The answers are :
5% : $3000
6% : $6000