Question

Write the equation of the line that passes through the given point and is perpendicular to the given line. (0,3); 3x – 4y = -8

Answer 1

First, we need to find the slope that we will use for our new line. We want it to be perpendicular to 3x-4y=-8, therefore we proceed to find the slope on this line:

`\begin{gathered} y=mx+b \\ \Rightarrow3x-4y=-8 \\ \Rightarrow3x=-8+4y \\ \Rightarrow3x+8=4y \\ \Rightarrow y=(3)/(4)x+(8)/(4)=(3)/(4)x+2 \\ m=(3)/(4) \end{gathered}`

We have that the slope of the line is m=3/4, then, for a perpendicular line, we need the negative inverse of this slope, we have then:

`\begin{gathered} m=(3)/(4)\Rightarrow m_p=-(1)/((3)/(4))=-(4)/(3) \\ m_p=-(4)/(3) \end{gathered}`

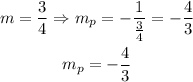
Finally, we use the point-slope formula to get the equation that we want:

`\begin{gathered} y-y_0=m(x-x_0) \\ (x_0,y_0)=(0,3) \\ \Rightarrow y-3=-(4)/(3)(x-0) \\ \Rightarrow y=-(4)/(3)x+3 \end{gathered}`

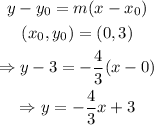
Therefore, the equation of the required line is y=-4/3x+3