Question

These figures are similar. Thearea of one is given. Find thearea of the other.3 inarea=24 in?6 in[ ? Jin?

Answer 1

Suppose that the dilation coefficient between two 2D figures is equal to k; therefore, the ratio between their corresponding sides is k. On the other hand, the ratio between the area of the two shapes is equal to k^2.

Therefore, in our case, the dilation coefficient is

`(6)/(3)=2=k\to\text{ dilation coefficient}`

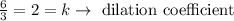
Then, as for the area,

`24=k^2A`

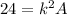
Where A is the area of the smaller figure.

Thus,

`\begin{gathered} \Rightarrow(24)/(k^2)=A \\ \Rightarrow A=(24)/(2^2)=(24)/(4)=6 \\ \Rightarrow A=6 \end{gathered}`

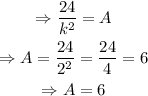
Therefore, the answer is 6in^2