Answer:
a) 17m, 24m, 33m, 44m, 57m
b) 7 m/s
c) 7m
d) 10m/s; 14m/s
e) 8
Step-by-step explanation:
Given:
d(t) = t² + 4t + 12 m
To find:
a. The position of the object after 1,2,3,4 and 5 seconds.
b. The average velocity of the object from 3 seconds to 4 seconds
c. The displacement from 1 second to 2 seconds.
d. The instantaneous velocity after 3 seconds and after 5 seconds.
e. The acceleration at t second/s.
a) To get the position after 1, 2, 3, 4, and 5 seconds, we will substitute t for 1, 2, 3, 4, and 5 respectively. This is because d(t) represents the postion at t seconds
d(1) = (1)² + 4(1) + 12 = 1 + 4 + 12 = 17m
d(2) = (2)² + 4(2) + 12 = 4 + 8 + 12 = 24m
d(3) = (3)² + 4(3) + 12 = 9 + 12 + 12 = 33m
d(4) = 4² + 4(4) + 12 = 44m
d(5) = 5² + 4(5)+ 12 = 57m
b) To get the average velocity of the object from 3 to 4 seconds, we will apply the formula:
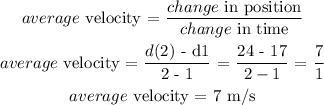
c) The displacement at 1 and 2 seconds respectively will be the difference of the positions at this time
d(2) = 24 m, d(1) = 17 m
displacement = d(2) - d(1) = 24 - 17
displacement = 7m
d) To get the instantaneous velocity, we need to first differentiate with respect to t.
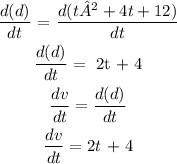
Then we will substitute t for 3 and 5 respectively.
dv/dt at t = 3 secs
dv/dt = 2(3) + 4 = 10 m/s
dv/dt at t = 5 secs
dv/dt = 2(5) + 4 = 14 m/s
e) To get acceleration, we will differentiate the function for the position with respect to t twice.
We did the first differential in instantenously velocity. We will differentiate the result again to get the acceleration with respect to t
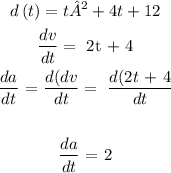
The value of our acceleration at t seconds is a constant. This means the acceleration will be constant throughout
Hence, the acceleration at t seconds = 8 (unit m/s²)