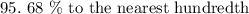SOLUTION:
Step 1:
In this question, we are given the following:
The average woman’s height is 65 inches with a standard deviation of 3.5 inches.
What proportion of women is shorter than 71 inches tall?
(enter the answer as a percent rounded to the nearest hundredth as needed)
Step 2:
The details of the solution are as follows:
Using the formulae, we have that:

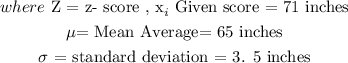
Step 3:
Computing the values, we have that:
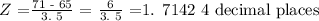
Now, we need to use the z-score calculator, to find the:
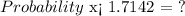
CONCLUSION:
The percentage of the women that are shorter than 71 inches tall is: