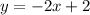The equation of a line has the form:
y=mx+b
We can find m by means of the formula:

Where (x1,y1) and (x2,y2) are points of the line.
In this case, we have the points (6,-10) and (-4,10), then we get:
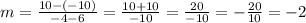
Now that we know that m= -2, we only need to find b, we can do it like this:
by taking the point (6,-10) replacing it into the equation and solving for b, we get:
-10 = -2*(6) + b
-10 = -12 + b
-10 +12 = b
b = 2
Then, the equation of this line is: