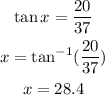Question

Trigonometry Match the following triangles with their missing values for variable x. ROUND TO THE NEAREST TENTH.

Answer 1

We have the following:

We can solve the triangles by means of the trigonometric ratios, which relate the hypotenuse with the legs.

The main trigonometric ratios are:

`\begin{gathered} \sin \theta=\frac{\text{opposite}}{\text{hypotenuse}} \\ \cos \theta=\frac{\text{adjacent}}{\text{hypotenuse}} \\ \tan \theta=\frac{\text{opposite}}{\text{adjacent}} \end{gathered}`

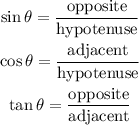
1.

To calculate the first triangle we must use the trigonometric cosine ratio, which relates the hypotenuse with the adjacent leg:

`\begin{gathered} \cos x=(8)/(11) \\ x=\cos ^(-1)((8)/(11)) \\ x=43.3 \end{gathered}`

2.

To calculate the first triangle we must use the trigonometric ratio sine, which relates the hypotenuse with the opposite leg

`\begin{gathered} \sin x=(15)/(24) \\ x=\sin ^(-1)((15)/(24)) \\ x=38.7 \end{gathered}`

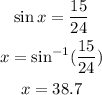
3.

To calculate the first triangle we must use the tangent trigonometric ratio, which relates the adjacent leg with the opposite leg

`\begin{gathered} \tan x=(20)/(37) \\ x=\tan ^(-1)((20)/(37)) \\ x=28.4 \end{gathered}`