Question

Calculate the area of a triangle with side lengths of 7ft ,8ft , and 9ft

Answer 1

Step1: Write out the lenght of the sides

`7ft,8ft\text{ and 9ft}`

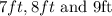
Step2; Calculate the semi perimeter of the triangle using the formula below

`\begin{gathered} s=(a+b+c)/(2) \\ \text{where = a, b, c are the lenght of the sides } \\ a=7,\text{ b=8, c=9} \\ s=\text{ semi-peremeter} \end{gathered}`

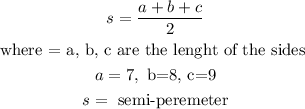
Then, by substituting the parameter, we have

`s=(7+8+9)/(2)=(24)/(2)=12`

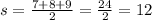
Step 3: Apply the heron's formula to find the Area

`\text{Area A=}\sqrt[]{s(s-a)(s-b)(s-c)}`

then substitute the parameters into the formula

`\begin{gathered} s=12,\text{ a=7, b=8, c=9} \\ \text{Area, A==}\sqrt[]{s(s-a)(s-b)(s-c)} \\ A=\sqrt[]{12(12-7)(12-8)(12-9)} \\ A=\sqrt[]{12*5*4*3} \\ A=\sqrt[]{720} \end{gathered}`

Then the area of the triangle is

`Area,A=12\sqrt[]{5}=26.83\text{ square unit}`