Question

Find the value for the voltage drop across each 15 Ohm resistor

Answer 1

Given:

The value of each resistance in parallel combination is,

`15.0\text{ ohm}`

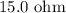
The value of the resistance in series with the parallel resistances is,

`10.0\text{ ohm}`

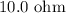
The potential drop across the battery is,

`45.0\text{ V}`

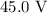
To find:

The voltage drop across each 15.0 ohm resistance

Step-by-step explanation:

The value of the equivalent resistance of the three parallel resistances is,

`\begin{gathered} (1)/(R)=(1)/(15.0)+(1)/(15.0)+(1)/(15.0) \\ (1)/(R)=(3)/(15.0) \\ R=(15.0)/(3) \\ R=5.0\text{ ohm} \end{gathered}`

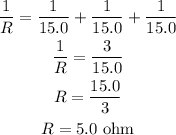
The net resistance of the circuit is,

`\begin{gathered} R_(net)=10.0+5.0 \\ =15.0\text{ ohm} \end{gathered}`

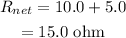
The circuit diagram is like this:

The current in the circuit is,

`\begin{gathered} I=(V)/(R_(net)) \\ =(45.0)/(15.0) \\ =3.0\text{ A} \end{gathered}`

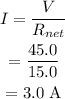
The potential drop across 10.0 ohm is,

`\begin{gathered} I*10.0 \\ =3.0*10.0 \\ =30.0\text{ V} \end{gathered}`

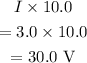
The potential drop across each of the 15.0 ohm resistance will be the same as the resistances are parallel.

So, the potential drop across each 15.0 ohm is,

`\begin{gathered} 45.0-30.0 \\ =15.0\text{ V} \end{gathered}`

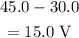
Hence, the required potential drop is 15.0 V.