Given:
(x + 1)(x - 5) = -9
Let's select the correct statement from the given options.
Equate the equation to zero by adding 9 to both sides of the equation:
(x + 1)(x- 5) + 9 = -9 + 9
(x + 1)(x - 5) + 9 = 0
Expand the left side using FOIL method:
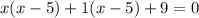
Apply distributive property:
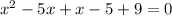
Combine like terms:
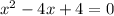
Factor using the perfect square rule:
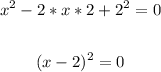
Thus, we have the factor:
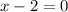
Therefore, the correct statement is: x - 2 = 0
ANSWER:
x - 2 = 0