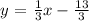Question

write an equation in slope intercept form for the line that passes through the given point and is perpendicular to the graph of the equation.(4,-3); y= 3x-5

Answer 1

Question:

write an equation in slope-intercept form for the line that passes through the given point and is perpendicular to the graph of the equation.

(4,-3); y= 3x-5​

Solution:

By definition, the slope-intercept form of a line is given by the following equation:

y = mx+b

where m is the slope of the line, and b is the y-coordinate of the y-intercept of the line. Now, if we have a perpendicular line to the line given by the equation y = mx+b, then we have that this perpendicular line has a slope 1/m (the reciprocal of the m).

Then, if we have a line given by equation

y = 3x-5

its slope is m = 3. And therefore, the slope of the line perpendicular to the above is m = 1/3. Then the slope-intercept of the perpendicular line is:

EQUATION 1:

`y\text{ = }(1)/(3)x+b`

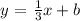
now, we need to find b. To find it take a point that passes through the line, for example (x,y) = (4,-3), and replace it in the above equation:

`-3\text{ = }(1)/(3)(4)+b`

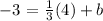
now, solve for b:

`b\text{ = -3 - }(4)/(3)=\text{ }(-13)/(3)`

Finally, replacing this value in equation 1, we obtain the slope-intercept form for the line:

`y\text{ = }(1)/(3)x-(13)/(3)`

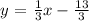
Then, we can conclude that the correct answer is:

`y\text{ = }(1)/(3)x-(13)/(3)`