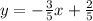SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the standard form for slope-intercept form for an equation of a line
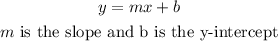
STEP 2: Write the first given equation
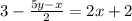
STEP 3: Simplify further to get the slope intercept form

Hence, the answer is given as: