Answer:
π/6 and 5π/6 radians
Explanations:
Given the trigonometry expression
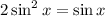
Let P = sin(x) to have:
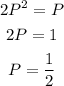
Substitute P = sin(x) into the resulting expression;
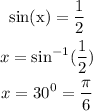
Since the equation is over the interval [0, 2 π) and sin(theta) is positive in the 2nd quadrant, hence other angles will be expressed as:
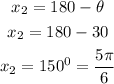
Therefore the exact solutions over the interval [0, 2 π) are π/6 and 5π/6 radians respectively