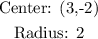Question

12. [Ex 2K) Find the centre, C, and the radius, r, of the following equation of circle: x2 + y2 - 6x + 4y + 9 = 0

Answer 1

An equation in the form:

`(x-a)^2+(y-b)^2=r^2`

is the standard form for the equation of a circle with center (a,b) and radius r. Here we have:

`x^2+y^2-6x+4y+9=0`

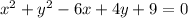
Then, group the x and y terms separately and "move" the constant to the right side of the equation:

`x^2-6x+y^2+4y=-9`

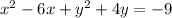
Complete the square:

`x^2-6x+9+y^2+4y+4=-9+9+4`

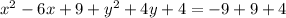
Factor:

`(x-3)^2+(y+2)^2=4`

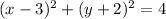
Express the right side as a square:

`(x-3)^2+(y-(-2))^2=2^2`

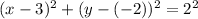
Therefore:

The center is: (3, - 2), the radius is 2

Answer:

`\begin{gathered} \text{Center: (3,-2)} \\ \text{Radius: 2} \end{gathered}`