Question

A. graph the system of inequalities. you may use the included coordinate plane or create one of your own. B. name one solution to the system C. is the ordered pair (1, 1) a solution to the system? why it why not?

Answer 1

A. The Slope-Intercept form of the equation of a line is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

• Given the first inequality:

`y>(1)/(3)x-2`

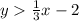
You know that the line is:

`y=(1)/(3)x-2`

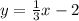
You can identify that:

`\begin{gathered} m_1=(1)/(3) \\ \\ b_1=-2 \end{gathered}`

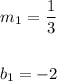
You can find the x-intercept by substituting this value into the equation:

`y=0`

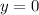
And then solve for "x":

`\begin{gathered} 0=(1)/(3)x-2 \\ \\ 2=(1)/(3)x \\ \\ (2)(3)=x \\ x=6 \end{gathered}`

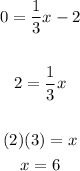
Then this line passes through this points:

`\begin{gathered} \mleft(0,-2\mright) \\ \mleft(6,0\mright) \end{gathered}`

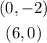
The symbol of the first inequality is:

`>`

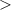
That means that you must graph a dashed line and the shaded region must be above the line.

Knowing the shown above, you can graph the line.

• Given the second inequality:

`2x+2y\ge8`

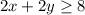
The line is:

`2x+2y=8`

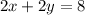
To find the y-intercept you must make

`x=0`

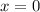
And solve for "y":

`\begin{gathered} 2(0)+2y=8 \\ \\ y=(8)/(2) \\ \\ y=4 \end{gathered}`

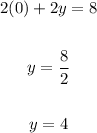
To find the x-intercept, substitute into the equation

`y=0`

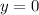
And solve for "x":

`\begin{gathered} 2x+2(0)=8 \\ 2x=8 \\ \\ x=(8)/(2) \\ \\ x=4 \end{gathered}`

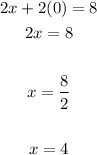
Therefore, the second line passes through these points:

`\begin{gathered} (0,4) \\ (4,0) \end{gathered}`

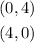
Since the symbol of the inequality is

`\ge`

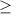
You must graph a solid line and the shaded region must be above the line.

The graph is:

B. The solutions of the System of inequalities are in the intersection region. Then, analyzing the graph, you can determine that this is one solution to the system:

`(5,5)`

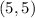
C. Having the ordered pair

`(1,1)`

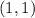
And observing the graph, you can see that it is not in the intersection region. Therefore, it is not a solution to the system.

The answers are:

A.

B.

`(5,5)`

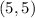
C. No, it is not. Because it is not in the intersection region.