Question

An airplane flies 200 km due west from city A to city B and then 280 km in the direction of 25.0° north of west from city B to city C.(a) In straight-line distance, how far is city C from city A? km(b) Relative to city A, in what direction is city C? ° north of west(c) Why is the answer only approximately correct?

Answer 1

First, let's draw a diagram representing the distances:

a)

To calculate the straight line distance, let's use the law of cosines, using the interior angle adjacent to the angle 25°, that is, an angle of 155°:

`\begin{gathered} a^2=b^2+c^2-2bc\cdot\cos155°\\ \\ a^2=200^2+280^2-2\cdot200\cdot280\cdot(-0.906)\\ \\ a^2=40000+78400+101472\\ \\ a^2=219872\\ \\ a=468.9\text{ km} \end{gathered}`

b)

Now, to find the direction, first let's decompose the 280 vector in horizontal and vertical components:

`\begin{gathered} V_x=280\cdot\cos25°=280\cdot0.906=253.68\\ \\ V_y=280\cdot\sin25°=280\cdot0.4226=118.33 \end{gathered}`

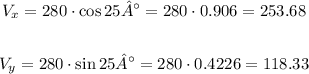
Now, let's add the horizontal component with the 200 vector, then calculate the angle of the resulting vector:

`\begin{gathered} V_x=253.68+200=453.68\\ \\ \theta=\tan^(-1)((V_y)/(V_x))=\tan^(-1)((118.33)/(453.68))=14.62° \end{gathered}`

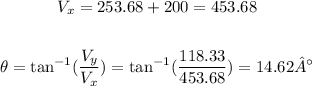
c)

The answer is approximately correct because the sine and cosine values used to calculate are not exact values, they are rounded values. Therefore the final result will not be 100% accurate.