Question

Looking to receive help on this practice question thank you!The first part is vertex form.

Answer 1

We have the following equation

`f(x)=x^2+8x+13`

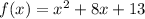
Since

`\begin{gathered} (x+4)^2=x^2+8x+16 \\ \text{then,} \\ x^2+8x=(x+4)^2-16 \end{gathered}`

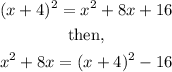
So, we can rewrite our equation as

`\begin{gathered} f(x)=(x+4)^2-16+13 \\ \text{which gives } \\ f(x)=(x+4)^2-3 \end{gathered}`

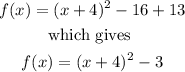
Then, the vertex form of our equation is:

`f(x)=(x+4)^2-3`

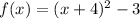
The graph of this equation is:

The general vertex form of a quadratic equatio is:

`\begin{gathered} y=a(x-h)^2+k \\ \text{with vertex (h,k)} \\ \end{gathered}`

By comparing this equation with our result, the vertex is:

`(x,f(x))=(-4,3)`

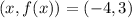
From the general vertex form, we know that the axis of symmtry is given by

`\begin{gathered} x=h \\ \end{gathered}`

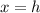
so, our axis of symmetry is x= -4.

The x-intercept ocurr at f(x)=0. Then, by subsituting this value into our function, we have

`0=(x+4)^2-3`

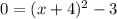
which leads to

`\begin{gathered} (x+4)^2=3 \\ x+4=\pm\sqrt[]{3} \\ x=-4\pm\sqrt[]{3} \end{gathered}`

which gives us two x-intercepts:

`\begin{gathered} x\text{ - intercept (small value) :} \\ x=-4-\sqrt[]{3} \\ x\text{ - intercept (large value value) :} \\ x=-4+\sqrt[]{3} \end{gathered}`