Question

What is the answer for this question?Find C. Then find the length and height of the storage shed?

Answer 1

`C=17x^2+(11662)/(x)`

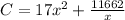
Given that:

Volume of the storage shed = 833 cubic feet

Cost of the concrete for the base per square foot = $8

Cost of concrete for the root per square foot = $9

Cost of the material for the sides per square foot = $3.50

Let x be the length of the side of the square and h be height of the shed.

The formula to calculate the volume is

V = Bh

where B is the base area.

Since the base is a square with side 'x',

`B=x^2`

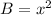
Substitute the given values into the formula of V.

`\begin{gathered} 833=x^2\cdot h \\ =x^2h \\ \Rightarrow h=(833)/(x^2) \end{gathered}`

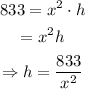
The base will have the same area with the roof.

Area of the roof = Base area

`=x^2`

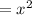
Cost to construct base

`=8x^2`

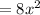
Cost to construct the roof

`=9x^2`

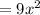
Area of one side = xh

Cost to construct one side = 3.5xh

Cost to construct 4 sides of the box

`\begin{gathered} =4(3.5xh) \\ =14xh \\ =14x\cdot(833)/(x^2) \\ =(11662)/(x) \end{gathered}`

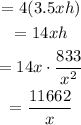
The total cost is the sum of these three costs. So, the objective function is

`\begin{gathered} C=8x^2+9x^2+(11662)/(x) \\ =17x^2+(11662)/(x) \end{gathered}`

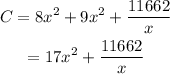
The dimension for the most economical cost will occur when dC/dx = 0. Then

`\begin{gathered} 34x-(11662)/(x^2)=0 \\ x^3=(11662)/(34) \\ =343 \\ x=7\text{ ft} \end{gathered}`

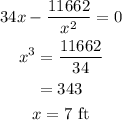
The length of side of the base is 7 feet.

Substitute the value of x into the equation of h.

`\begin{gathered} h=(833)/(7^2) \\ =17\text{ ft} \end{gathered}`

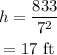
The height of the storage shed is 17 feet.