1.
80% means eighty out of every hundred.
This way, the fraction would be:
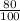
Simplifying,
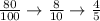
Note: Notice that eighty out of every hundred, eight out of every ten and four out of every five mean all the same: 80%
2.
3/8 means three out of every eight. To convert this to a percentage we can use a rule of three, taking 8 as the 100% as following:
This way,

Therefore, 3/8 as a percentage would be 37.5%