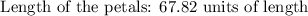Hello there. To solve this question, we'll have to remember some properties about polar curves and lengths of parameterized curves.
Given the following polar curve defined as:
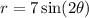
First, remember that for the polar curve
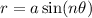
The number of petals defined by n depends on its parity:
If n is even, we have 2n petals.
If n is odd, we have n petals.
For example, compare
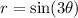
The graph is as follows:
And the graph of

Its graph is
Okay. So in the case of the polar curve in the question, first note that it has a amplitude of 7 (that is, the distance between the origin and the farthest point from it in a petal is 7)
And it might have 4 petals, hence its graph is:
Notice that the line passing through one petal is the line representing the angle pi/4.
To solve for the arc length, we use the following formula:
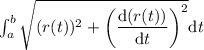
Where a and b are the angles in which the petal is between.
In this case, we'll calculate half of it, integrating from the angle it starts up to pi/4. Hence, doubling the result, we get the final answer.
In this case, we find the intersection of it with the origin making:
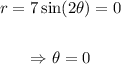
Integrating it up to pi/4, we get:
![\begin{gathered} \int_0^{(\pi)/(4)}2\cdot√((7\sin(2\theta))^2+\left[\left(7\sin(2\theta)\right)'\right]^2)\,\mathrm{d}t \\ \\ \int_0^{(\pi)/(4)}2\cdot√(49\sin^2(2\theta)+196\cos^2(2\theta))\,\mathrm{d}t \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/j9aqxpdc33woii0nkucwdx0zouz9ccuzww.png)
Notice we can rewrite the radical as:
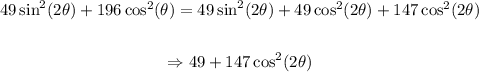
Such that we get:
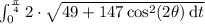
Whereas
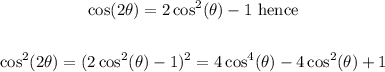
Therefore we get
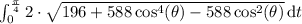
Since we want the measure of all the petals, we multiply this result by 4, hence we get the following approximation: