Let x be the cost for the small pizza and y the cost for the medium one. We know that 3 small ones and 3 medium ones cost $51, this can be express as:
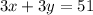
we also know that 5 small ones and 2 medium ones cost $55, this means that:
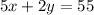
Then we have the system of equations:
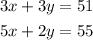
Multipliyng the first equation by 2 and the second by -3 we have:
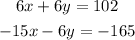
Adding the equations we have:
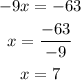
Once we know the value of x we plug it in the first equation and solve for y, then:
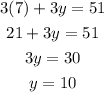
Hence, a small pizza cost $7 and a medium one cost $10.
now that we have the cost of each of them we can obtained the cost for 3 small and 2 medium:
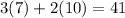
Therefore, 3 small and 2 medium pizzas cost $41. The answer is C.