Given the parabola:
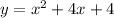
a = 1
b = 4
c = 4
The x-coordinate of the vertex is found as follows:
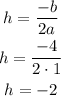
The x-coordinate of the vertex is found as follows:
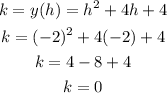
Then, the vertex is (-2, 0)
The y-intercept is found as follows:
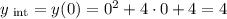
The y-intercept is (0,4)
The vertical line: x = h, in this case x = -2 is the symmetry axis. Then the point
(-4, 4) is on the parabola. With these 3 points, we can plot the function. The graph is: