Question

determine whether the Mean Value Theorem can be applied to f on the closed interval [a,b]. If the Mean Value Theorem can be applied, find all values of in the open interval such that

Answer 1

Given:

The function

`f(x)=(x)/(x-5),\text{ on interval}[1,4]`

Required:

Dermine whether the Mean Value Theorem can be applied to f on the closed interval [a,b]. If the Mean Value Theorem can be applied, find all values of in the open interval .

Step-by-step explanation:

`\begin{gathered} \text{The mean value theorem states that for a continuous and differentiable} \\ \text{ function }f(x)\text{ on the interval }[a,b],\text{ there exists such number }c\text{ from } \\ \text{ interval }(a,b),\text{ that }f^(\prime)(c)=(f(b)-f(a))/(b-a). \end{gathered}`

First, evaluate the function at the endpoints of the interval:

`\begin{gathered} f(4)=-4 \\ f(1)=-(1)/(4) \end{gathered}`

Next, find the derivative

`\begin{gathered} f^(\prime)(c)=-(c)/((c-5)^2)+(1)/(c-5) \\ =((-4)-(-(1)/(4)))/((4)-(1)) \\ Simplify: \\ -(c)/((c-5)^2)+(1)/(c-5)=-(5)/(4) \\ Sol\text{ve the equation on the given interval}:c=3 \end{gathered}`

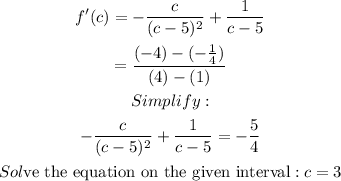
Answer:

The value of c = 3.