Vector representation:
Let vector A be;
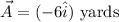
Vector B be;
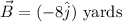
Vector C be;
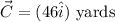
The resultant displacement vector R is given as,
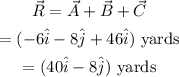
The magnitude of the resultant displacement vector is given as,
![\begin{gathered} \lvert\vec{R}\rvert=\sqrt[]{(40)^2+(-8)^2} \\ \approx40.79\text{ yards} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/whl4819sxj6t2aoic08b5pesvmp7v9fci4.png)
Therefore, the magnitude of the football's resultant displacement is 40.79 yards.