The given sequence is
48, 24, 12, 6, ...
Let a be the first term of the given sequence.
a=48.
we need to find the common ratio.
consider the first two terms.
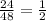
Consider the terms 24 and 12.
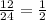
The common ratio is 1/2.
The given sequence is in the form of geometric progress.
Recall that the formula for the n th term of G.P is
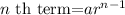
Substitute a=48, r=1/2, and n=8 to find the 8 th term.
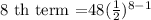
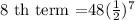
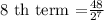
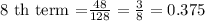
Hence the 8 th term of the given sequence is 3/8 or 0.4.