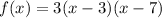 Step-by-step explanation
Step-by-step explanationThe intercept form of a quadratic equation is
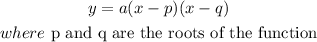
so
Step 1
find p and q values
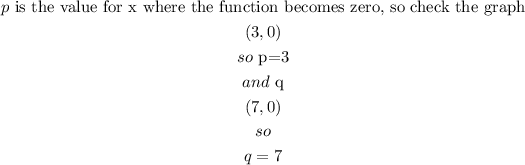
p=3
q=7
Step 2
now, to find the a value we need another point of the graph
check the vertex , it is
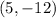
so, replace
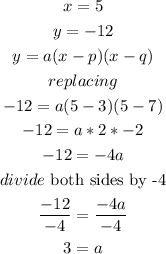
so
a=3
therefore, replacing in the formula we have the answer
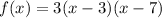
I hope this helps you