Given:
The radioactive substances uranium-240 has a half-life of 14 hours. The amount A(t) of a sample of uranium-240 remaining (in grams ) after t hours is given by the following exponential function:
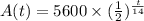
To know:
Find the initial amount in the sample and the amount remaining after 30 hours.
Step-by-step explanation:
Initial amount will be at t =0 and at t = ti time.
Solution:
We will take function A(t), at t=0 initial amount
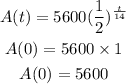
And at t = 30 hours
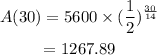
Hence, 1267.89 gram is the answer.