Question

Quadratic Equations: Use the discriminate, b^2 - 4ac, to determine the number of solutions of the following quadratic equation. Then solve the quadratic equation using the FORMULA ATTACHED (picture) This is the problem: -y^2 - 36 = -12y

Answer 1

We have the equation:

`-y^2-36=-12y`

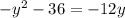
let's write in the standard form to identify the values of the constants:

`y^2-12y+36=0`

from this we notice that a=1, b=-12 and c=36. Plugging this values into the discriminant we have:

`(-12)^2-4(1)(36)=144-144=0`

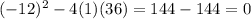
Since the discriminant is equal to zero that means that the equation has only one solution of multiplicity 2.

Let's find the solution with the general formula; plugging the values of a, b and c we have:

`\begin{gathered} y=\frac{-(-12)\pm\sqrt[]{(-12)-4(1)(36)}}{2(1)} \\ =\frac{12\pm\sqrt[]{0}}{2} \\ =(12)/(2) \\ =6 \end{gathered}`

Therefore the solution of the equation is 6.