Question

Ty has a total of $5.40 in quarters and pennies in his wallet. He has two times as manypennies as he does quarters. How many of each coin does he have?

Answer 1

From the question, we can deduce the folllowing:

Total amount = $5.40

Number of pennies = two times the number of quarters.

We have:

P = 2Q

Let's find the amount of each coin he has.

Let P represent the number of pennies

Let Q represent the number of quarters.

Where:

1 penny = $0.01

1 quarter = $0.25

We have the set of equations:

0.01P + 0.25Q = 5.40............................equation 1

P = 2Q.......................................................equation 2

Let's solve the system of equations using substitution method.

Substitute 2Q for P in equation 1:

0.01(2Q) + 0.25Q = 5.40

0.02Q + 0.25Q = 5.40

Combine like terms:

0.27Q = 5.40

Divide both sides by 0,27:

`\begin{gathered} (0.27Q)/(0.27)=(5.40)/(0.27) \\ \\ Q=20 \end{gathered}`

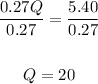
Now, substitute 20 for Q in equation 2:

P = 2Q

P = 2(20)

P = 40

We have the solutions:

P = 40, Q = 20

Therefore, Ty has 40 pennies and 20 quarters.

ANSWER:

Quarters = 20

Pennies = 40