Question

Convert the polar equation r = 2 secØ to a Cartesian equation.y = 2x = 2x^2 = 2

Answer 1

Polar and cartesian equation

Initial explanation

Let's analyze the relation between r and x and y:

We have that between the indicated value of r (of the polar coordinates) and x and y (of the cartesian coordinates) there is a relation because they form a triangle. If r changes, then the value of x and y will change.

STEP 1: given equation

Using the given equation

r = 2 secØ

we have that

`\begin{gathered} r=2secØ \\ \downarrow \\ (r)/(2)=secØ \end{gathered}`

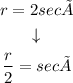
STEP 2: secØ equation

Observing the image of the initial explanation we have a right triangle, we know that the equation of

secØ for any right triangle is given by:

`\sec Ø=\frac{\text{hypotenuse}}{\text{adjacent side}}`

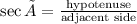
In this case,

hypotenuse = r

adjacent side = x

then,

`\begin{gathered} \sec Ø=\frac{\text{hypotenuse}}{\text{adjacent side}}=(r)/(x) \\ \sec Ø=(r)/(x) \end{gathered}`

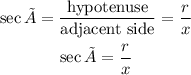
STEP 3: comparison between given equation and secØ equation

Then, we have that:

`\begin{gathered} \sec Ø=(r)/(x) \\ \sec Ø=(r)/(2) \end{gathered}`

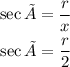
This means that:

`\begin{gathered} (r)/(x)=\sec Ø=(r)/(2) \\ \downarrow \\ (r)/(x)=(r)/(2) \end{gathered}`

Then,

x = 2

The equation in cartesian coordinates is x=2.

Answer: x=2