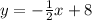Question

Find the equation of a line that is perpendicular to y=2x+1 and passes through the point (4,6).

Answer 1

A perpendicular line has a negative reciprocal, that is,

`\begin{gathered} M=-(1)/(m) \\ \text{where, in our case, m=2 (the coefficient of x).} \end{gathered}`

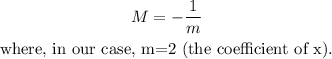
Then, the slope M of the perpendicular lines is

`M=-(1)/(2)`

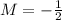
then, the perpendicular line has the form

`y=-(1)/(2)x+b`

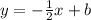
where b is the y-intercept. We can find b by subtituting the given point, that is,

`\begin{gathered} \text{subsituting point (4,6) into the last equation, we get} \\ 6=-(1)/(2)(4)+b \end{gathered}`

which gives

`6=-2+b`

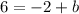
and by moving -2 to the right hand side, we have

`\begin{gathered} 6+2=b \\ 8=b \\ or\text{ equivalently,} \\ b=8 \end{gathered}`

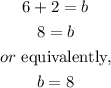
Therefore, the perpendicular line is

`y=-(1)/(2)x+8`