First, we write the equation and balance it:
Na2S (s) + Pb(NO3)2 (aq) → 2NaNO3 (aq) + PbS (s) (1)
The reactants:
1) 8.75 g Na2S (s)
The molar mass of Na2S =78.0 g/mol
2) 250 mL of 0.400 mol/L Pb(NO3)2 (aq), we need the mass:
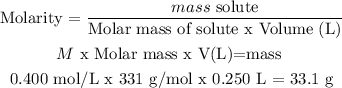
The molar mass of Pb(NO3)2 (aq) = 331 g/mol
Volume = 250 mL = 0.250 L
The mass of Pb(NO3)2 (aq) = 33.1 g
Note: we must determine the limiting reactant first.
--------------------------------------------------------------------------------------------------------------
The limiting reactant
"We have 8.75 g Na2S and 33.1 g Pb(NO3)2"
Using stoichiometry and reaction (1),
The molar mass of Na2S =78.0 g/mol
The molar mass of Pb(NO3)2 (aq) = 331 g/mol
78.0 g Na2S ---------- 331 g Pb(NO3)2
8.75 g Na2S ---------- x
x= 37.1 g Pb(NO3)2
Conclusion: For 8.75 g of N2S we need 37.1 g Pb(NO3)2, and according to 2) we only have 33.1 g, we have less than we need, so the limiting reactant is Pb(NO3)2.
---------------------------------------------------------------------------------------------------------------
The mass of PbS (s)
We already know the limiting reactant, Pb(NO3)2.
The molar mass of PbS = 239 g/moll
Procedure:
331 g Pb(NO3)2 --------- 239 g PbS
33.1 g Pb(NO3)2--------- y
y= 23.9 g PbS
Answer: Mass of PbS = 23.9 g