Question

If gtx) = -2(x + 5)² +3, which statement is true?OA. The axis of symmetry of x) is x = 5, and the axis of symmetry of gtx) is x = 5.OB. The axis of symmetry of (x) is x = 5, and the axis of symmetry of gtx) is x = -5.OC. The axis of symmetry of x) is x=-5, and the axis of symmetry of gtx) is x = -5.OD. The axis of symmetry of f(x) is x=-5, and the axis of symmetry of gtx) is x = 5,

Answer 1

Given the graph of f(x) and the function:

`g(x)=-2(x+5)^2+3`

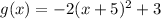
You need to remember that, by definition, the Axis of Symmetry of a parabola passes through its vertex, and divides the parabola into two equal parts.

• You can identify in the graph that the vertex of the parabola is its maximum point:

`(5,3)`

Therefore, you can draw the vertical lines that pass through the vertex:

Notice that the x-coordinate of each point on the line is always the x-coordinate of the vertex of the parabola. Therefore, the equation for that line is:

`x=5`

• In order to find the Axis of Symmetry of g(x), you need to rewrite it in this form:

`g(x)=ax^2+bx+c`

By definition:

`(a+b)^2=a^2+2ab+b^2`

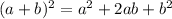
Therefore, you can expand the function:

`g(x)=-2(x^2+2(x)(5)+5^2)+3`
`g(x)=-2(x^2+10x+25)+3`
`g(x)=-2x^2-20x-50+3`
`g(x)=-2x^2-20x-47`

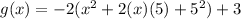
Now you can find the Axis of Symmetry using this formula:

`x=-(b)/(2a)`

In this case:

`\begin{gathered} a=-2 \\ b=-20 \end{gathered}`

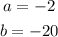
Then, you get:

`\begin{gathered} x=-((-20))/(2(-2)) \\ \\ x=-5 \end{gathered}`

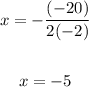
Hence, the answer is: Option B.