Question

The length of a rectangle is three more than twice the width. The perimeter is 102. What are the dimensions?

Answer 1

Let

Length of rectangle be "x"

Width of rectangle be "y"

Given, length is 3 more than twice width, we can write:

`x=2y+3`

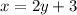
Also, given the perimeter is 102.

Recall, perimeter is sum of all the sides of a rectangle. Thus, we can write:

`\begin{gathered} x+y+x+y=102 \\ 2x+2y=102 \end{gathered}`

Substituting, equation 1 into equation 2, we get:

`\begin{gathered} 2x+2y=102 \\ 2(2y+3)+2y=102 \end{gathered}`

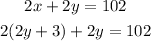
Multiplying out and solving for y:

`\begin{gathered} 2(2y+3)+2y=102 \\ 4y+6+2y=102 \\ 6y=102-6 \\ 6y=96 \\ y=16 \end{gathered}`

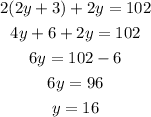
Now, x is:

`\begin{gathered} x=2y+3 \\ x=2(16)+3 \\ x=32+3 \\ x=35 \end{gathered}`

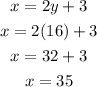
Answer:

The length is 35 and width is 16