Question

Assume that when adults with smartphones are randomly selected, 54% use them in meetings or classes. If 7 adult smartphone users are randomlyselected, find the probability that at least 5 of them use their smartphones in meetings or classes.The probability is(Round to four decimal places as needed.)

Answer 1

Let's list down the given information the question.

Probability of success p (smartphone users) = 54%

probability of failure q (non-smartphone users) = 100% - 54% = 46%

n = 7

To be able to get the probability of at least 5 out 7 uses smartphones in the meetings, we will have to solve the probability of getting exactly 5, 6, and 7 smartphone users and add the results.

The formula to use is:

`P(x)=nCx* p^x* q^(n-x)`

where p, q, and n were already defined above and x = the number of success.

Let's begin calculating the probability of x = 5 smartphone users. Let's plug in the values of n, x, p, and q in the formula above.

`\begin{gathered} P(5)=7C5*0.54^5*0.46^2 \\ P(5)=21*0.0459165*0.2116 \\ P(5)=0.2040346 \end{gathered}`

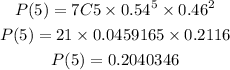
The probability of getting exactly 5 smartphone users is 0.2040346.

Let's solve for the probability of x = 6 smartphone users. Plugging in the values of n, x, p, and q, we get:

`\begin{gathered} P(6)=7C6*0.54^6*0.46^1 \\ P(6)=7*0.0247949*0.46 \\ P(6)=0.079839 \end{gathered}`

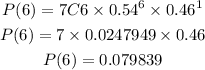
The probability of getting exactly 6 smartphone users is 0.079839.

Lastly, let's solve for the probability of x = 7 smartphone users. Plugging in the values of n, x, p, and q, we get:

`\begin{gathered} P(7)=7C7*0.54^7*0.46^0 \\ P(7)=1*0.013389*1 \\ P(7)=0.013389 \end{gathered}`

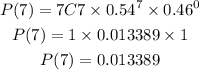
The probability of getting exactly 7 smartphone users is 0.013389.

As mentioned, to get the probability of at least 5 out 7 uses smartphones in the meetings, we will have to solve the probability of getting exactly 5, 6, and 7 smartphone users and add the results.

`\begin{gathered} P(x\ge5)=P(5)+P(6)+P(7) \\ P(x\ge5)=0.2040346+0.079839+0.013389_{} \\ P(x\ge5)=0.2973 \end{gathered}`

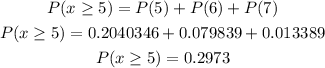
Therefore, the probability of at least 5 out 7 randomly uses smartphones in the meeting is 0.2973.