Question

Need help with the exercise , don’t understand what to start with

Answer 1

We need to find the legs of a right triangle.

We know that one of the acute angles is 45º. Since the three internal angles of any triangle must add up to 180º, the other angle A is given by:

`\begin{gathered} A+45\degree+90\degree=180\degree \\ \\ A+135\degree=180\degree \\ \\ A+135\degree-135\degree=180\degree-135\degree \\ \\ A=45\degree \end{gathered}`

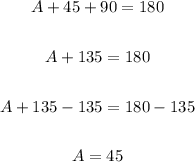
So, both acute angles measure 45º. Since those angles are congruent, so are the legs of the triangle.

Now, calling x the length of each leg, we can use the Pythagorean Theorem to find:

`\begin{gathered} (leg_1)^2+(leg_2)^2=(\text{ hypotenuse})^(2) \\ \\ x^(2)+x^(2)=4^(2) \\ \\ 2x^(2)=4^(2) \\ \\ (2x^2)/(2)=(4^2)/(2) \\ \\ x^(2)=(4^2)/(2) \\ \\ \sqrt[]{x^(2)}=\sqrt[]{(4^2)/(2)} \\ \\ x=\frac{4}{\sqrt[]{2}} \end{gathered}`

Therefore, the lengths of the legs are:

`\frac{4}{\sqrt[]{2}}`