Given a closed box with a square base of side length l feet, height h feet, and volume 31 cubic feet.
To find the surface area, we would need to find the height of the closed box in terms of l. We can use the formula below.
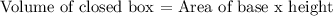
Therefore,
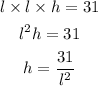
From the result above, we can then proceed to get the expression for the surface area of the box.
In this case, the surface area would be given by the formula below;
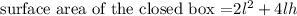
We would substitute the value of "h" into the above equation;
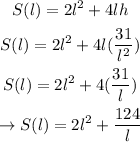
Therefore, the surface area of the closed box in terms of "l" is
Answer: Option 2